2021. 3. 31. 14:18ㆍ프로그래밍-코딩테스트/LeetCode

inorder traversal와 preorder traversal한 데이터가 들어왔을때 트리를 그리라는 뜻
간단하게 정리하자면 Preorder는 root->left->right 순으로 순회를,
Inorder는 left->root->right 순으로 순회를 하는 것이다.
각 traversal 결과에 대해 root를 기준으로 정리할 수 있다.
예컨데 preorder의 경우 root node를 가장 먼저 방문하므로, 3이 root가 되고
이를 inorder에 적용하면 3을 기준으로 9가 left node, 15,20,7은 right node라는 것을 알 수 있다.
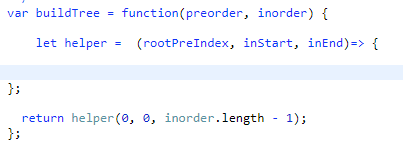
따라서 다음과 같은 방식으로 문제를 풀어보려 한다
helper라는 함수를 이용하여 재귀처리 하려고 한다. 이때 사용되는 args는 rootPreIndex, inStart, inEnd이다.
rootPreIndex는 pre배열에서 root 노드의 위치가 되고, inorder 배열은 inStart부터 inEnd까지의 범위를 순회하게 된다.
즉, root를 pre배열에서 찾아낸 후, inorder로 subtree의 범위를 정하여 순회하는 것이다.

1) preorder에서 root 노드를 찾는다. preorder는 항상 0번째 노드가 전체 트리의 root 노드이다. 또한 이 값은 rootVal에 저장한다.
2) inorder에서 root노드의 위치를 찾는다. 이를 rootInIndex라고 한다.
3) 2에서 구한 inorder의 index를 기준으로, 왼쪽은 left subtree, 오른쪽은 right subtree가 된다.
이제 각 subtree에 대한 재귀를 실행한다. 여기부터 예시로 설명한다.

4) left subtree: pre의 0번째 element가 root임을 알았으므로, +1번째는 left subtree의 root노드가 될 것이다. 이렇게 이전 root노드에 1을 더해주면 left subtree의 root node가 된다.

이때 left subtree가 스캔해야되는 노드는 inorder의 0번째 배열부터 새로 찾아낸 root 전까지의 범위이다. 따라서 instart와 rootInIndex-1을 범위인자로 넘겨준다.
5) right subtree : 4와 동일하지만 배열의 길이가 n인 inorder에 대해 left subtree가 0~root-1번째 원소 까지였다면, right는 root+1부터 n까지가 스캔 범위가 된다.
따라서 4에서 스캔하는 left subtree의 길이를 rootPreIndex에 더해주면 다음 재귀의 rootPreIndex값이 될 것이다. 왜냐하면 pre배열은 root-left-right순으로 배치되어있으므로, rootPreIndex+left subtree의 길이 위치의 원소가 right의 첫 node가 되기 때문이다.

해당 문제에서는 이를 leftCount라 표현하였다.
이렇게 설정한 후 right도 재귀를 돌린다.
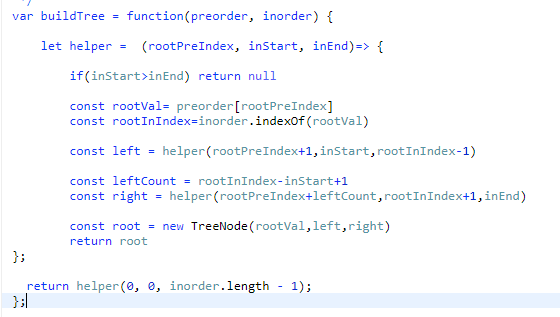
최종적으로 만들어진 root를 각각 node에 만들어주면 된다.
'프로그래밍-코딩테스트 > LeetCode' 카테고리의 다른 글
| [Recursion] Letter Combinations of a Phone Number (0) | 2021.03.31 |
|---|---|
| [Array] Sort Colors (0) | 2021.03.31 |
| [Tree] Flatten Binary Tree to Linked List (0) | 2021.03.29 |
| [Array] Container With Most Water (0) | 2021.03.29 |
| [Stack] Decode String (0) | 2021.03.29 |